25.09.2021

Математические закономерности в растениях

Если спросить обычного человека, а не ученого, есть ли какая-нибудь связь между растениями и математикой, то вряд ли он придумает что-то, кроме простого счета. Двадцать ромашек минус двенадцать гладиолусов получается… А ничего не получается!

Попробуем взглянуть на эту тему по-другому. И начнем исследование с древности. Ведь не может быть, чтобы такой вопрос не возникал раньше.

Математические закономерности в природе в целом и в растениях в частности интересовали ученых начиная с Древней Греции. Вернее, вполне возможно, что подобные вопросы возникали у мудрецов Древнего Египта и Вавилона, но письменные источники об этом до нас не дошли.

Знаменитый древнегреческий философ Пифагор (6 в. до н. э.) считал, что основа всего сущего - это число. Платон (5-4 вв. до н. э.) полагал, что есть идеальные формы, а природные объекты - это только их несовершенные отображения. Так круглый цветок - только приближенное значение идеального круга. А Теофраст (4-3 вв. до н. э.) отмечал, что если у растения плоские листья, то они расположены на ветке в правильном ряду.

Все это нам мало поможет разобраться. Конечно, число и форма - это математические понятия, но древнегреческие мыслители используют их в философском смысле.

В 1202 году ученый Леонардо Фибоначчи написал труд “Книга абака”, где среди прочего написал свою знаменитую последовательность цифр, названная его именем. Числа Фибоначчи неожиданно оказались связаны с растениями. Спираль, построенная по числам Фибоначчи выглядит так:

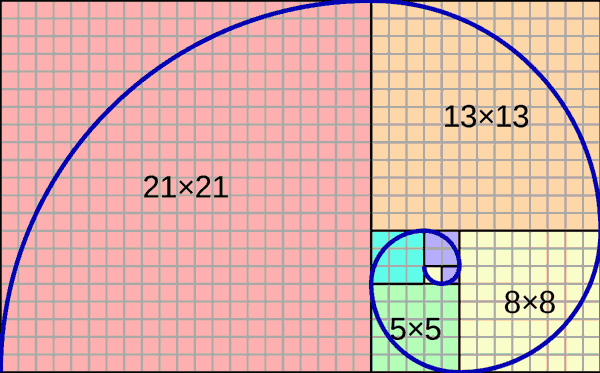
https://en.wikipedia.org/wiki/Fibonacci_number#/media/File:FibonacciSpiral.svg

А вот спирали Фибоначчи, которые явно видны в строении листьев алоэ:

https://ru.wikipedia.org/wiki/Геометрические_закономерности_в_природе#/media/Файл:Aloe_polyphylla_spiral.jpg

Числа Фибоначчи встречаются в растениях повсеместно - в расположении листьев на ветке и ветвей на дереве, в строении ростков ананаса и цветках артишока, в молодом разворачивающемся листе папоротника и так далее.

Это только один способ, которым математики объясняют форму природных объектов, в том числе растений. Еще для этого используется теория хаоса, логарифмические спирали, фракталы и еще много других страшных и непонятных слов для неспециалиста. Но они не одни описывают эти закономерности - есть и влияние физики.

Сложность понятий не должна отпугивать тех, кто стремиться к новым знаниям. Давайте рассмотрим некоторые математические закономерности на примерах.

Например, фракталы - это бесконечные самоподобные и повторяющиеся математические конструкции. Это в идеале, а в природе бесконечность самоповторения возможна только в воображении. Если эти слова кажутся чересчур сложными, то взгляните на распространенный пример фрактального строения среди растений - на брокколи Романеско:

https://en.wikipedia.org/wiki/Patterns_in_nature#/media/File:Romanesco_broccoli_(Brassica_oleracea).jpg

Также фракталы встречаются в ветвлении баобаба, а также в листьях зонтичных растений и папоротников.

Или вот еще математическая закономерность с понятным названием, которое большинство людей знает еще с детства: мозаика - узор на плоской поверхности, образованный повторяющимися плитками. В природе встречается достаточно часто - к примеру, чешуя рыб или соты пчел. Среди растений тоже можно найти образец - цветок рябчика шахматного:

https://en.wikipedia.org/wiki/Patterns_in_nature#/media/File:Fritillaria-meleagris-blomst.JPG

Математические закономерности очень интересно прослеживать на природных объектах. Так наука из умозрительной становится четкой и систематической, что только способствует запоминанию у начинающих (студентов или тех, для кого знания - это хобби).

Ни для кого не секрет, что математика - это сложный предмет, в котором нельзя ничего пропускать. Что же делать, если нужен реферат по алгебре и математике в целом, а тема пропущена? Лучший выход - обратиться за помощью к специалистам. Например, на сайт Zachete.ru, где привыкли побеждать любые проблемы с учебой.

Люся Елисеева